¿Cuántos décimos tienes que comprar para que te toque la lotería? Estos matemáticos dicen tener la respuesta
Investigadores de la Universidad de Manchester han desarrollado un método geométrico que garantiza obtener un premio... pero no cubrir las pérdidas

Un participante en un sorteo selecciona los números a jugar. / Getty

Un sueño para muchos y una pérdida de tiempo para otros, la lotería es un elemento troncal en muchas sociedades; y en especial, en España, un país que cada 22 de diciembre tiene a gran parte de su población pegada a sus pantallas para escuchar los números que cantan los niños de San Ildefonso. ¿Es posible calcular cuántos décimos o boletos hay que comprar para garantizar ganar algo en este tipo de sorteos?
Más información
Un grupo de matemáticos de la Universidad de Manchester cree que sí. Basándose en 'Lotto', el principal juego de la Lotería Nacional de Reino Unido, en el que se extraen números aleatorios entre el 1 y el 59, David Stewart y David Cushing calcularon que el número mínimo de intentos para tener garantías de conseguir un premio es 27. Sin embargo, introducen un matiz importante: conseguir un premio al intento 27 no garantiza rentabilizar el gasto inicial.
Para llegar a esta conclusión, los matemáticos han utilizado un sistema matemático conocido como geometría finita, un modelo geométrico basado en una estructura similar a un triángulo llamada plano de Fano. Cada punto de esta estructura se traza con pares de números y se conecta con líneas, de tal manera que cada línea genera un conjunto de seis números. En este caso, estos seis números equivalen a un boleto. Se necesitan tres planos de Fano y dos triángulos para cubrir los 59 números y generar 27 combinaciones.

Ejemplo de geometría finita.
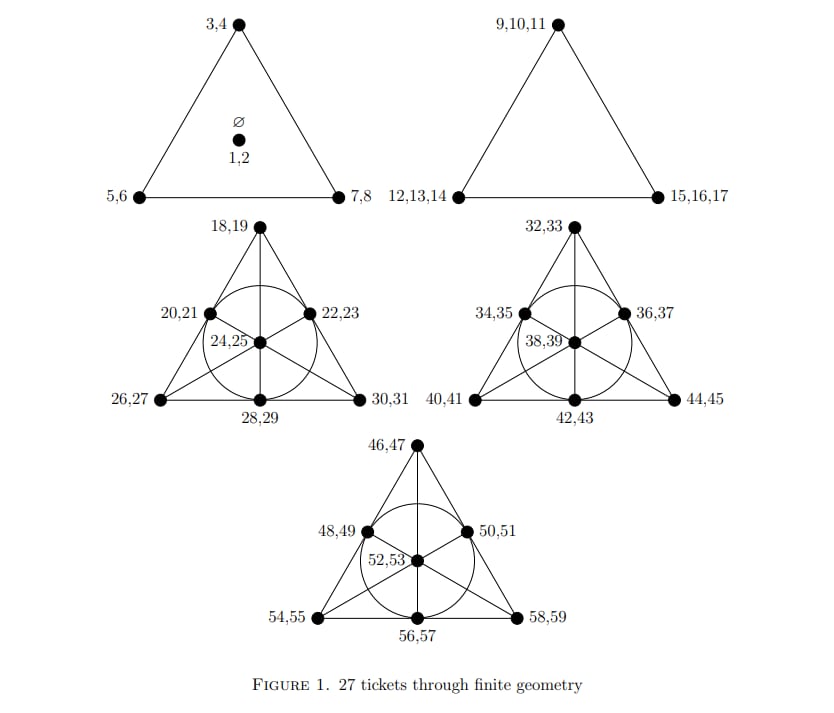
Ejemplo de geometría finita.
Según estos matemáticos, elegir los números con los que jugar basándose en este modelo geométrico garantiza que, sin importar cuál de los 45.057.474 sorteos posibles ocurra, uno de los boletos tendrá, al menos, dos números en común. "En cualquier sorteo de seis números, dos números deben aparecer en una de las cinco estructuras geométricas, lo que asegura que aparezcan en al menos un boleto", aseguran en un comunicado.
Para Stewart y Cushing, lo que este trabajo demuestra es que no es posible lograr el mismo resultado con 26 boletos. "Fundamentalmente, existe una tensión que proviene del hecho de que sólo hay 156 números en 26 boletos. Esto significa que muchos números no pueden aparecer muchas veces. De esta manera, podrá encontrar seis números que no aparecen en ningún boleto juntos. En términos de teoría de grafos, terminamos demostrando la existencia de un conjunto independiente de tamaño seis".
Prueba en un sorteo real
Dado que cada boleto cuesta 2 libras, los matemáticos necesitarían gastar 54 libras para garantizar la obtención de un premio. No obstante, los investigadore afirman que las posibilidades de obtener ganancias son muy poco probables, ya que en el 99% de los casos no se recuperaría el dinero. A este respecto, subrayan que sus estimaciones no deben usarse como una razón para participar en juegos de azar.
Los investigadores no se han quedado en la teoría. Al poner a prueba su método en el sorteo correspondiente al 1 de julio de 2023, acertaron sólo dos bolas en tres de los boletos. El premio fueron tres boletos para el siguiente sorteo. Ninguno de ellos resultó agraciado.
En cualquier caso, sostienen que su hallagzo es interesante desde el punto de vista computacional. Para el estudio, usaron un lenguaje de programación de hace 50 años llamado Prolog; en sus propias palabras "uno de los ejemplos más antiguos de inteligencia artificial real".






